I’m done with chapter 3 in Carroll’s book, although I still have to go through the problems at the end. Some of these will be quite tricky, if the problems in previous chapters are any indication. I already got quite a workout from following the explanations in the text, as Carroll leaves lots of details up to the reader. In particular, I spent a couple of days trying to understand the derivation he makes of the Riemann curvature tensor, \(R^{\rho}_{\,\,\sigma \mu \nu}\). This tensor completely defines the curvature of a surface, and a space is geometrically flat when it equals zero. This tensor is one of the main players in General Relativity, and is defined as \[ R^{\rho}_{\,\,\sigma \mu \nu} = \partial_{\mu}\Gamma^{\rho}_{\sigma\nu}-\partial_{\nu}\Gamma^{\rho}_{\sigma\mu}+\Gamma^{\rho}_{\lambda\mu}\Gamma^{\lambda}_{\sigma\nu}-\Gamma^{\rho}_{\lambda\nu}\Gamma^{\lambda}_{\sigma\mu} .\]
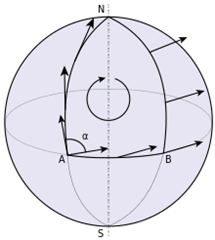
I stole the image here from the Wikipedia article to ilustrate the concept of parallel transport: you start out with a vector at a point A, as in the picture, and keep the vector pointing along the path you follow along the surface (here, northward along a meridian on a sphere). If you then turn towards another path and make your way back to your starting point, you will find that on a curved surface the vector you dragged along has been rotated. This happens in surfaces that are intrinsically curved, and the Riemann tensor is a measure of that curvature. Typically, the strategy to derive \(R^{\rho}_{\,\,\sigma \mu \nu}\) is to imagine doing the parallel transport along an infinitesimal rectangular area, as is done in the book by Schutz. Carroll, however, goes for a more direct, but also much more abstract derivation: if you have the commutator of a covariant derivative acting on a vector field, you end up with a neat expression, after some work, that includes the Riemann tensor as part of the result: \[ [\nabla_{\mu},\nabla_{\nu}]V^{\rho} = R^{\rho}_{\,\,\sigma \mu \nu}V^{\sigma} – 2\,T^{\lambda}_{\,\,\,\mu \nu}\nabla_{\lambda}V^{\rho} .\]
The term \( T^{\lambda}_{\,\,\,\mu \nu} \) is the torsion tensor, which was previously introduced in the chapter. So what we have is that when taking the (covariant) derivative of a vector field in two different directions, it matters which direction you pick first. This only happens in curved spaces, where you end up with vectors being tilted with respect to the direction they had when they first started out. Carroll does the demonstration of this in three lines, and hand-waves a bit about how to get from one line to the next. So, I took it as practice to reproduce the derivation myself, and found I was successful, without the aid of the text book, after three attempts. Typing the whole thing would be impossible here, but fortunately I did take a picture (click to enlarge):
The definitions for the covariant derivatives of vectors and one-forms are in the box in the upper right corner, and the derivation begins on the upper left. On the lower left is just a reminder to myself of the definition of an anti-symmetrized tensor, which I used in the next-to-last line. The whole thing took about half an hour, with constant erasing and starting over at several points—as it should be. A valuable lesson, then, is that following the text and constructing the arguments yourself pays off in valuable practice; you can anchor your results in the steps that the author does show, and work out the entrails of the calculation yourself. As an added bounus, often times the end-of-chapter problems ask you to “fill in the missing steps in the derivation of equation X”, so you can tick problems off your set (indeed, I have been able to check many problems in Schutz’s book off my list this way).

No comments:
Post a Comment