Back to work tomorrow

As was the case last week, I did a lot of resting and reading this past week. This time, I finished (and will write a review of) Jerry Coyne's Why Evolution is True. I've always felt my knowledge of evolution was pretty robust, and generally I found a lot of the book was a review for me, but there were several gems and interesting facts I didn't know before. Overall, it's a very accessible (and very well researched) book for anyone who has gaps to fill in their understanding (at a laymen level) of evolution. I will also post the review for this book on my other website sometime soon, as I feel that there's hardly any discussion of many issues that I think are important, or that merely seem interesting to me, in Spanish. As soon as that review is done, I'm probably going to be unable to read much for pleasure for some time, but I want to get to Coyne's other book, Faith Versus Fact, which I have on my shelf as well.

I also downloaded and installed the free, open-source software Inkscape. The idea behind this is I want to produce physics posts that include good-looking graphics, plus I want to avoid stealing images from other people: I'd sleep better making my own. From what I see at the gallery at the Inkspace website, the tool may be overkill for drawing pulleys and incline planes, but I want to try it out anyway. Another option that I have on the table is learning how to use the tikz and pgfplots pakages in LaTeX, which I'm familiar with. I feel that software like Inkscape could achieve many of the same results with a friendlier learning curve, though of course it would be suicide to use it for plotting mathematical functions. (I used good ol' Paint for some graphics in earlier posts, and was not too happy with the result. What I want is something that's easily usable like Paint, but with prettier results.)

A week of reading and rest

I'm finally working up the will to actually use my break from University to do some academic work, after a full week of rest and reading. If there's something I miss from the time I wasn't a PhD student, it's the time I had for literature of all kinds. Last Spring break I used the time to catch up on reading as well, and found it rewarding. So far, I've completed Ernst Jünger's Storm of Steel, and I'm looking at my bookshelves already to pick my next book.

Storm is a fascinating document, basically a polished diary of one German soldier's experience in World War I. I've encountered another version of this kind of literature before in All Quiet on the Western Front, by Erich Maria Remarque. I read that more than a year ago, and might re-read it soon, but I remember that that book is a much more "novelized" account of many of the same events. Unlike Remarque, Jünger passes no judgement of the causes of the war, nor does he mention any of the politics of the era at all. He simply tells what things happened to him, without much in the way of what he thought about them.

Both books left me amazed at the sheer amount of shelling that the war unleashed; it seems hardly a page goes by without "we came under heavy artillery fire". After a couple hundred pages of being under artillery fire (representing more than four years for Jünger) you wonder how it could be that anyone could survive the conflict and not be traumatized: just search YouTube for "world war 1 shell shock" and brace yourself.

I want to write a proper review of Storm of Steel, but I'm doing it in Spanish at my other site. For now, it is enough to state that it is a must-read for anyone interested in WWI, 20th Century history, or the combat experience in general. Accounts by historians are always useful, and I've read some myself, but Storm is a very polished primary source.

UPDATE 08/09/2016: the review is here (en español).

July 31, 2016

I'm sorry I'm late with this post, in case you're keeping track so far. Life gets in the way sometimes, and there's just not enough time to do everything I want to do. Anyway, I'm reading Storm of Steel, by Ernst Jünger, and it's fascinating. It's a WWI book by a German soldier who survived the entire war, often in some of the biggest battles for months at a time, and then went on to be a prolific author and die aged 102! I've read some things on WWI before, but this is another level in terms of the crudeness of the conflict. Jünger's book is famous for not editorializing much, and simply telling things as they happen. He doesn't go into the reasons for the conflict, or whether or not it was just, or any of the comments you see in other WW1 literature. He just tells, in honest detail, what the soldiers went through. I'm about halfway through at this point, and I think I'll finish it by midweek.

Thoughts for July 23, 2016

Walking with PhD buddies on our way to lunch earlier this week, one of us mentioned the various atrocious and tragic events that have happened over the last couple of weeks. One of my buddies, who is from Chile, jokingly remarked: "All of a sudden, Mexico doesn't seem that bad anymore, huh?" We all had a good chuckle, and carried on towards our meal.

There's a saying among some comedians, which I think may itself be rooted in a quote from Oscar Wilde, that to be funny one must be telling the truth. Mexico has a myriad problems, from the daily life of its citizens all the way up to macroeconomic issues. But when one looks at international headlines, at least from the comfort of a middle-class PhD student, Mexico really isn't all that bad at all.

Europe is turning into a huge 1980's Beirut or, as some others have remarked, modern day Israel. There are now constant attacks by competing islamists against Jews (largely underreported), and ordinary citizens (especially women), not to mention the large-scale attacks like the ones in Nice last week. The Middle East, it seems, has found a way to make its troubles more horrifying and, on top of that, to export them. It doesn't help that Turkey is having an Islamic Revolution of its own, and may finally descend into full islamic theocracy soon. Syria is so bad that it's barely even reported anymore, except as a tally of dead and displaced that goes up every day. As I write this, there is news of a blast in Kabul, Afghanistan, carried out by ISIS militants against a Shia protest. To top everything off, the American election is one huge joke, with a competition between a plastic candidate that will change nothing and a dangerous, narcissistic idiot on the other.

So yes, Mexico is quite comfortable for now, from where I'm sitting (big caveat there!).

Thoughts for the week, July 16

My actual PhD work is coming along slowly but steadily. I've briefly mentioned my general area of study, which is General Relativity(GR) and, in particular, an approach to Quantum Gravity known as Causal Dynamic Triangulations (CDT). I've thought of writing something about this, but I can do no better than the explanation of the subject at The Physics Mill. There's a lot of good stuff over there and Jonah, the author, is much further along this area of study than I am (I do not know him in any world, real or virtual).

I can, however, explain a little bit of what I'm trying to do or, at least, what my professor has me working on at present. The idea is that, according to a proposed model of spacetime, we can have an elementary "cell" that divides into other spacetime cells, and those cells each divide as well, and so on. Each cell is a tiny, four-dimensional spacetime pyramid called a simplex. The way to keep track of the divisions is to keep track of the vertices, which is a lot easier, since each vertex is just a point. Simplex division in this case follows a specific set of rules: for example, the distance between any two vertices has to be greater than or equal to a minimum length, \(l\). This is the consequence of insisting that spacetime be quantized, which is the whole point of what CDT is about: we want to get tiny, indivisible chunks of spacetime that, when seen from far away, look like the smooth, continuous spacetime that GR describes.

My job, then, is to use computational methods to put a specific model of CDT to the test. The paper that outlines this model, sadly, is behind a paywall, but related papers on the physics arxiv are here and here. Anyway, here is a preliminary result:

I know, I know, it's not very impressive—but it took hours and hours of coding! An obvious remark would be that this is only a three dimensional spacetime, since that's what can be plotted in an image. This 3-D version of spacetime is a proxy for the real, 4-D thing that can't be visualized. The radius of the sphere that contains the vertices increases by a magnitude equal to the minimum length \(l\) at each step, and each step is a quantum "tick" of time. The mechanism by which the points divide is by "mating" with other points according to a specific operation and generating a new point at the new radius. All points mate with all other points, and the resulting points are located on the next sphere. This creates an enormous number of points that can't possibly fit on the surface of the sphere and maintain the condition that the distance between them is at least \(l\), so points are eliminated one by one until this condition is met (you can see the number of points in each stage at the top of the figure).

*   *   *

On completely different topics, this has been a tumultuous week. There was the attack in Nice, France, and the attempted military coup in Turkey. I wish I could write about these events, but I'm still overwhelmed by the amount of information to be digested in order to write something worth reading. 

Weekly thoughts, July 8: Gun control

In case you are interested, the view from Mexico about the gun control situation in the U.S. is, actually, not that trivially aligned with that of the wider world. I am an atypical Mexican in that I follow political and social developments in other countries closely, especially in the anglosphere. There's a common stereotype that Americans know nothing of the outside world, but I can assure you, if you're an American reader, that Mexicans are comparably ignorant about or--perhaps understandably--busy with other things besides world politics. So I can give a detailed picture about what I think, for what it's worth, but only some general remarks about Mexican society.

First, I find it scandalous that nothing has been done about the problem at all.  One would think that even the most rabid gun nut would acknowledge that something has to be done, but they actually double down and insist on "the cost of freedom" or some other platitude, and sometimes simply quote the final four words of the Second Amendment, "...shall not be infringed!", as if that were a knock-down argument for any gun control.  The trivial reply from someone like me would be, "well, then change what your stupid second amendment says!" It just seems incredible that, in the couple of decades that I've been paying attention, nothing has been done at all. Indeed, things have gotten somewhat worse since the assault weapons ban expired in the late 90's: yes, assault weapons account for only a tiny percentage of deaths, as most are due to handguns, but that's no consolation to the people in Aurora or Orlando. Yes, I understand how lobbying works and that the NRA does a lot of it; yes, I know there's a "gun culture" in the US that's different from that in some European countries with widespread gun ownership; yes, I know there are 300 million guns already out there and prohibition will create a black market and all of that; and yes, obviously some components of the problem are due to mental illness and religious terrorism; but still, the answer from Americans is we should do nothing?

From what I understand, most Americans actually do want to do something, like basic background checks before gun purchases and closing the gun-show loophole. But these things don't even get discussed at the political level because the gun nuts are very well organized in their lobbying via the NRA. I don't see Americans mobilizing en masse to do some effective lobbying of their own, as this would require a broad spectrum of warring groups in the culture war to cooperate extensively. Perhaps they could rally behind a strong presidential candidate with lots of political capital, but then that's not going to happen in this election. Over 30,000 annual deaths, plus the high-impact mass shootings we see every few months, have simply not been enough to get legislators to grow a pair and do something.

This sentiment of bewilderment at the situation is shared by most educated people in Mexico, though many laypeople who read of the latest mass shooting simply shrug it off with "Well, we all know Americans are crazy. So of course one of them would walk into an elementary school and kill 20 kids and their teachers at some point. That's just what Americans do." There is another strand of thought, if we could call it that, that seems to want to have something like the 2^nd amendment here in Mexico. Gun ownership by citizens is regulated in theory, with citizens being able to own handguns up to a .38 caliber. Everything else is deemed "for exclusive use of the army." Very few Mexicans go through the hoops necessary to get legal ownership of a gun, though those hoops are purely bureaucratic and have nothing at all to do with training in the use of firearms.

In practice, Mexico is flooded with illegal guns, which come mostly from the US and are owned by the cartels. There have been cases of .50 caliber machine guns, grenades, and rocket launchers found in the hands of the narcos; they usually out-gun the police and sometimes even the army. Still, ordinary citizens tend to shy away from gun ownership, except for the small but growing group that I mentioned above: these people, usually right-leaning or anarchist, speak of "the people" taking arms and overthrowing the corrupt government, as they perceive that every other thing has been tried already and failed. There is also a strong current of vigilantism that advocates for citizens doing police work, as police in Mexico are generally regarded as worse than the criminals.

I don't think these Mexican NRA-types will have anything in the form of political success anytime soon, but I do worry about the vigilantism they inspire. There are already cases of mobs lynching suspected criminals, and there's no way that could get any better if the mobs were armed with guns instead of pitchforks. Politicians, especially at the local levels, have already been subject to attacks usually attributed to organized crime. I can't see how that would get any better if any Joe Schmo (or Juan Pérez, rather) could do the same as well. Domestic violence deaths, suicides, and accidents would obviously increase, too. I'm by no means a pacifist--I'm just squeamish about people self-righteously appointing themselves as "good guys with guns" with no one even writing their name down somewhere.

Weekly Summary: July 1, 2016

I’m done with chapter 3 in Carroll’s book, although I still have to go through the problems at the end. Some of these will be quite tricky, if the problems in previous chapters are any indication. I already got quite a workout from following the explanations in the text, as Carroll leaves lots of details up to the reader. In particular, I spent a couple of days trying to understand the derivation he makes of the Riemann curvature tensor, \(R^{\rho}_{\,\,\sigma \mu \nu}\). This tensor completely defines the curvature of a surface, and a space is geometrically flat when it equals zero. This tensor is one of the main players in General Relativity, and is defined as \[ R^{\rho}_{\,\,\sigma \mu \nu} = \partial_{\mu}\Gamma^{\rho}_{\sigma\nu}-\partial_{\nu}\Gamma^{\rho}_{\sigma\mu}+\Gamma^{\rho}_{\lambda\mu}\Gamma^{\lambda}_{\sigma\nu}-\Gamma^{\rho}_{\lambda\nu}\Gamma^{\lambda}_{\sigma\mu} .\]

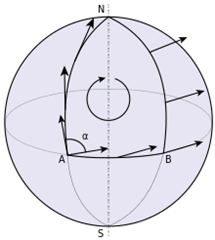
I stole the image here from the Wikipedia article to ilustrate the concept of parallel transport: you start out with a vector at a point A, as in the picture, and keep the vector pointing along the path you follow along the surface (here, northward along a meridian on a sphere). If you then turn towards another path and make your way back to your starting point, you will find that on a curved surface the vector you dragged along has been rotated. This happens in surfaces that are intrinsically curved, and the Riemann tensor is a measure of that curvature. Typically, the strategy to derive \(R^{\rho}_{\,\,\sigma \mu \nu}\) is to imagine doing the parallel transport along an infinitesimal rectangular area, as is done in the book by Schutz. Carroll, however, goes for a more direct, but also much more abstract derivation: if you have the commutator of a covariant derivative acting on a vector field, you end up with a neat expression, after some work, that includes the Riemann tensor as part of the result: \[ [\nabla_{\mu},\nabla_{\nu}]V^{\rho} = R^{\rho}_{\,\,\sigma \mu \nu}V^{\sigma} – 2\,T^{\lambda}_{\,\,\,\mu \nu}\nabla_{\lambda}V^{\rho} .\]

The term \( T^{\lambda}_{\,\,\,\mu \nu} \) is the torsion tensor, which was previously introduced in the chapter. So what we have is that when taking the (covariant) derivative of a vector field in two different directions, it matters which direction you pick first. This only happens in curved spaces, where you end up with vectors being tilted with respect to the direction they had when they first started out. Carroll does the demonstration of this in three lines, and hand-waves a bit about how to get from one line to the next. So, I took it as practice to reproduce the derivation myself, and found I was successful, without the aid of the text book, after three attempts. Typing the whole thing would be impossible here, but fortunately I did take a picture (click to enlarge):

The definitions for the covariant derivatives of vectors and one-forms are in the box in the upper right corner, and the derivation begins on the upper left. On the lower left is just a reminder to myself of the definition of an anti-symmetrized tensor, which I used in the next-to-last line. The whole thing took about half an hour, with constant erasing and starting over at several points—as it should be. A valuable lesson, then, is that following the text and constructing the arguments yourself pays off in valuable practice; you can anchor your results in the steps that the author does show, and work out the entrails of the calculation yourself. As an added bounus, often times the end-of-chapter problems ask you to “fill in the missing steps in the derivation of equation X”, so you can tick problems off your set (indeed, I have been able to check many problems in Schutz’s book off my list this way).

Weekly summary: June 24

So, in my effort to neglect this blog a little less, and to help myself battle procrastination a bit, I'll try to post weekly about things on my mind and things I got done along the week. My idea is to do this on Fridays and, if all goes well, this will be the beginning of a long trend of regular posting (not that I have that many readers yet, but that's kind of the point).

Anyway, the big news today is definitely Brexit, with a narrow majority of Brits voting to leave the EU. I don't know what to say about this, as Mexico isn't, and never has been, in a similar situation. From what I see on social media--particularly Twitter--people who voted to leave the EU are labeled de facto bigots, whereas people who voted to remain are branded as corrupt, self-hating authoritarians.  What seems to be unambiguous is the dismay of the scientific community at the situation. The impact around the world will play out slowly over the next few months, but already there are warnings from experts of future financial and, potentially, political turmoil. For now, Mexican technocrats have used Brexit as an excuse to pass budgetary cuts--no one believes them, as always, and they go ahead anyway, as always.

Speaking of Mexico, the news out of the southern state of Oaxaca made headlines around the world and, as is usually the case anytime Mexico is noticed internationally, it was bad news. Teachers protested last weekend over an education reform that was passed a couple of years ago and has been phased into practice since. The crux of the issue is that the government insists that teachers need to be evaluated, but the teachers insist that the evaluation methods are extremely unfair and hurt teachers in poorer states and neighborhoods the most. Last Sunday, teachers protested and were met by riot police that had been waiting for them. The riot police were accompanied by hundreds of armed federal agents. Nobody knows who started the violence, but eventually shots were fired and eight people died; over a hundred more were wounded. Each side accuses the other of starting the violence, and there is no clear path forward at the time. Oaxaca is one of the poorest states in Mexico, and the teacher's union (known as the CNTE) is particularly strong there; there are frequent protests, especially around the month of May, when teacher's day is celebrated in Mexico. The CNTE union is known for its massive national mobilizations and month-long strikes in Oaxaca, and the educational reform has made them more upset than usual--rightly so, I think.

Federal agents in riot gear confront protesters in Oaxaca, Mexico.

*   *   *

Anyway, on the Physics side of things, I had a modestly productive week. I'm working my way through Carroll's text, Spacetime and Geometry, specifically the third chapter on curvature. As a backup, I went back to the book by Schutz, which is a couple notches below Carroll's in difficulty and has many, more 'basic' exercises. Curvature is a big deal in General Relativity, since gravity is understood as an effect of geometry rather than a force. We're all familiar with curved surfaces and objects, such as basketballs and the Earth's surface; the idea in GR is that spacetime is curved, and what we perceive as gravity is the manifestation of that curvature.

More specifically, on curved, continuous surfaces (known technically as manifolds) one has to account for the way coordinates are bent and twisted along with the surface. Up/down, left/right, forward/backward, and past/future point in different directions depending on where one is, and how one is moving. Specifying coordinates and higher concepts such as velocities or trajectories is much harder than in the regular, flat geometry we all are used to. It is necessary, then, to introduce geometrical concepts that are much more general than those of Euclidean (i.e., flat) geometry, and to generalize calculus accordingly as well. As an example, the derivative for a vector looks like this in generalized curved coordinates: \[\frac{\partial \vec{V}}{\partial x^\beta} = \frac{\partial V^\alpha}{\partial x^\beta }\vec{e}_{\alpha}+\frac{\partial \vec{e}_\alpha}{\partial x^\beta }V^\alpha.\]  In flat cartesian coordinates the second term is always zero, since the basis vectors \( \vec{e}_\alpha\) are constant (they're just unit vectors always pointing in the \(x\), \(y\), and \(z\) directions) and their derivative is zero. But in general curvilinear coordinates, the basis vectors change along a path; they get twisted, turned, or stretched on different parts of the surface. In general, these changes that the basis vectors undergo (the term \(\frac{\partial \vec{e}_\alpha}{\partial x^\beta }\) above) can be written as a linear combination of some coefficients that act upon the basis vectors. These coefficients can be written as mathematical gizmos that look like this: \[ \frac{\partial \vec{e}_\alpha}{\partial x^\beta } = \Gamma^{\mu}_{\,\,\,\alpha \beta} \vec{e}_\mu.\] These gizmos are known as Christoffel symbols, and what they do is adjust for how the basis vectors \(\vec{e}_\mu\) change along the curvature of the surface. So, for the above vector \(\vec(V)\), the derivative can now be written as \[\frac{\partial \vec{V}}{\partial x^\beta} = \left( \frac{\partial V^\alpha}{\partial x^\beta }+V^\mu\,\Gamma^{\alpha}_{\,\,\,\mu\beta} \right )\vec{e}_{\alpha}.\]

Armed with these gizmos, we can generalize ordinary vector calculus operations to curved space. The problem is where to get them in the first place! Luckily, they can be calculated from the metric of the manifold: this is the one defining characteristic for the manifold's curved character, and is usually written in the form of an equation for what the line element (a typical, small line that lives in the manifold) looks like. The line element for the surface of a sphere, for example, is fairly dull: \[ ds^2 = r^2\,d\theta^2 + r^2 \sin^2\theta \, d\phi^2.\] (Notice we only need to specify two angles, latitude and longitude, to move along the surface of the sphere; once you live on a sphere and are confined to move along it's surface, the radius is not much use, that's why there's no \(dr^2\) term.) Once we have the equation for the metric, and after we write it in matrix form \(g\), we can calculate the coefficients according to \[ \Gamma^{\gamma}_{\,\,\,\beta \alpha} = \frac{1}{2}g^{\alpha \gamma} \left( \partial_\mu g_{\alpha\beta} + \partial_\beta g_{\alpha\mu} - \partial_\alpha g_{\beta\mu} \right).\]

Obviously I've glossed over a lot of things, pulled things from under my sleeve, and generally omitted lots of details. Eventually I'll explain these things in much grater detail and include pictures for these things so it'll become clearer what it is I'm talking about, but I have to learn to use the tikz and pgfplots \(LaTeX\) packages properly, which takes some time. Anyway, if all goes well, I'll have something to write about next week at the latest.

On the Quantum God of the Gaps

I recently listened to an episode of the Atheistically Speaking podcast on the subject of Einstein's and Gödel's belief (or lack thereof) in God.  The podcast overall is quite enjoyable and going strong after more than 200 episodes; I've only started listening in the past few weeks and have been alternating between listening to new and archived episodes. At a point in this particular show, the host (Thomas) and his guest (Kurt) quite literally say: "Hey, if there's a physicist out there listening to this, let us know what you think..." So, this post is the result of taking them at their word, given that so much of the show had me shaking my head throughout. I should also mention that Thomas was kind enough to invite me to write to him directly, and the following is a slightly polished version of the e-mail I sent him. Here we go:

Quantum Mechanics (QM) is part of a core of courses that all physicists take, no matter what their field. Obviously, people who specialize in QM will get into it a lot deeper than those that don't. There are some complicated areas of research going on right now, and there's plenty of debate going on--but the "basics", if we could call them that, are more than enough to refute just about everything Kurt said on episode 242.

First, the easy point: if you're going  to take the approach "some smart guy believes X, so X is true" your're already in trouble because, as Bertrand Russell said, if you rely on an authority for your argument, there will always be other authorities who disagree. So if we were to tally the John Polkinghornes of the world as evidence that there could be a god hiding somewhere in QM--or free will, or the soul, or whatever--, then we would have to be intellectually honest and tally all the other guys who say he's full of shit as evidence that there's no such thing, which is everybody else. People in this latter camp include Sean Carroll, Lawrence Krauss, Richard Feynman, Tim Maudlin, Steven Weinberg, and many others. Polkinghorne is a theologian, so he's intellectually compromised by definition. This is not an ad-hominem: this is a simple statement of the fact that he can't be relied upon to be intellectually honest. If he were, he wouldn't be a theologian.

Now, on to actual QM: Just as in high-school algebra we had some complicated equation with numbers and letters, and we were asked to solve for "x", so too in QM there's an equation to solve, only mere algebra won't quite do the trick. This is the Schrödinger equation, which looks something like this: \[ i \hbar \frac{\partial \Psi}{\partial t} = -\frac{\hbar^2}{2m} \frac{\partial^2 \Psi}{\partial x^2} + V\Psi. \]
It may look complicated, but the idea is the same as in high school algebra: solve for the wave function, \(\Psi\) (greek letter "Psi").  After you do that, what you will get is an equation for \(\Psi\) that tells you what its value is in terms of x (position) and t (plain old time), plus some other physical constants and the specifics of your system (these are included in the V term above). Just as "x" was uniquely determined by all the other variables in high-school algebra, so too is \(\Psi\) determined--fully, for all time--by all the other squiggles in the Schrödinger equation. This is a second-degree partial differential equation and, with the right input, is fully deterministic.

The subtlety arises in the fact that \(\Psi\) is not a number, but a probability density, and that's where laymen get mixed up. Here is where an analogy will help and, if you were to remember any part of this post as particularly useful, this would be it. Imagine you have a fair die that you can throw. For any given throw, it's pretty hard to know what number is going to come up. Naively, one would think that the die coughs up a random number between 1 and 6 each time. However, if you throw the die many times, eventually you'll see a pattern: each number comes up roughly 1/6 of the time. That 1/6 is determined by the geometry of the die. No matter what individual result you look at--1,4,2,5,3,etc.--the 1/6 is always the same for every throw. That 1/6, roughly, is \(\Psi\). The geometry of the die is everything else in the Schrödinger equation. So even though any given throw is undetermined, the overall 1/6 is fixed for as long as the geometry is fixed.

Every experiment ever done confirms that the above equation, or some version of it, is true. If Kurt  (or Polkinghorne, or whoever) wants to say that god is hiding somewhere in \(\Psi\), then they're making a claim that god can do no better that to show up as what probability theory would predict anyway without him, which seems like a pretty lame god to me.

As if that weren't enough, there's an entire field of research on hidden variable theory--the idea that there is a more fundamental, fully deterministic physics underneath the probabilistic character of the wave function. So the statement by Kurt, that it's just "a brute fact that QM is this way" is not obviously true either. Anyway, on to Gödel:

First, the necessary caveat: I'm a physicist, not a mathematician. With that said, Gödel's incompleteness theorems state that, for any given mathematical system based on arithmetic and axioms, there will be one of two inevitable outcomes: 1) there will be some theorems that will be true but unprovable, or 2) all theorems will be provable, but some will contradict others.

As an example, consider the sentence

"This statement is true".

Each word there is well-defined and fits the usual syntax to create a meaningful idea. You can think of each one of these words as an axiom (a basic assumption that doesn't need to be proven), and the syntax is the logic that is used to put them together and derive a theorem, which is a conclusion--the meaning of the statement itself. However, we can follow the same axioms and rules to construct a statement like this:

"This statement is false."

Each word there is well-defined, and all the words are arranged properly, but we can't decide on the meaning of the statement because the content of the statement refutes its logical construction!

Now, even though this is certainly important for the philosophy of mathematics, there is no way that you can get from it to the claim made by Kurt that some things are, and always will be, unknowable. That's a non-sequitur at worst, and a trivial argument from ignorance at best. A key distinction to keep in mind is that unprovable does not mean unknowable: remember, item 1) for the incompleteness theorems says "true, but not provable". In a way, this is part of what theoretical physics is about: there are some things we know are true (thanks to experiment) and we work to explain them--that is, to prove why it must be the case that they are true.

In any case, when people speak of god, they always mess up and fall into contradictions in the axioms themselves.  Their conclusions are unsound because their premises are gibberish and the arguments never get off the ground--there are no theorems to be derived at all! This happens to all definitions of god that include omnipotence, for example. Once they include that as a basic assumption, the rest is white noise.

Thomas covered other many other areas of disagreement with Kurt on the show itself, and some commenters on the episode site have done so as well, so I'll leave it here for now. As a conclusion, I would say that people aren't smuggling contraband into QM (god, free will, the soul, consciousness) as much as they're smuggling it into their misunderstanding of QM. Sometimes, these people even have PhD's and published peer-reviewed papers. Bad ideas in science are weeded out eventually, but someone has to actually get on the ground and do it. This must be done by the experts, but it can be a slow, thankless process and so most of them just stay out of it and focus on their research; only a few jump in and get down and dirty. In the meantime, one has to be patient and wait it out.

I’m still alive!

So, my last post was a few months ago, which is a surprise to me, since I have felt as if I’ve only been away for a couple of weeks. Well, that’s what diving into General Relativity will do to you, I guess. Anyway, the point is I’ve been busy, but I’ve constantly thought of resuming regular posting on physics and all kinds of other things here. I’ve finally felt guilty enough to at least post this and, as I write, I don’t really know what to say other that I’ll do my best to neglect this blog a little less. (I’ve managed a handful of posts in my other blog, in Spanish, but even posting over there is too scarce for my taste as well.)

Most of the CUCEI campus is reing renovated, which means lots of dust all over the place, but the renovations will be worth it, as far as I can tell. For example, in order to get to the graduate physics building, I have to get through this:

The tiny gray structure behind the (brand new) yellow building is Building Z, where I and other graduate physics students dwell on campus. Other parts of CUCEI are quite lovely, and the students are quite peaceful and dedicated to their studies. Here are a few samples:

Also, I’ve made a somewhat successful effort  to exercise. I jog for a few minutes on the track a few minutes’ walk from Building Z. Sometimes I can get a short run on three weekdays, though mostly I get one or two and another one on the weekend.

This track was just renovated as well, so I’ll be running on a nice new track starting next week.

Anyway, as far as actual physics goes, I’m almost done with a “first pass” over Relativity. I’ve used the textbooks by Lambourne, Schutz, and Carroll. Lambourne is surprisingly easy to digest, thought it may be too lenient for some people’s taste. Schutz is more like the usual modern approach to Relativity at the undergrad level, and Carroll is much more advanced and directed explicitly at graduates.

I’ve been assigned to write a short essay explaining de Sitter space for my Relativity course, and the text is pretty much ready (though in Spanish). If all goes well, I’ll resume posting here regularly quite soon, and I’ll use that essay as a crutch to get started. After that, I hope to resume topics on Classical Mechanics, and then work my way into other core subjects of graduate physics. Perhaps I’ll do asides on mathematical concepts as well, and many other topics that interest me (politics, religion, books, philosophy). This is a blog, after all, and I’m sort of making it up as I go along. In an ideal world with plenty of time and no procrastination, I would have a physics/math post and an unrelated post each week. I know I’m supposed to focus on my studies, but I just love writing and hate leaving for (possibly several years) later.

First week in PhD

So I'm in the middle of my first week of my Physics PhD, at least officially, since the semester began this past Monday. I'd been spending time at the campus since last week, just getting started planning things with my adviser and getting used to the facilities. I actually like the CUCEI campus quite a lot, but it's been undergoing heavy renovation for a few weeks now, and I'd prefer to wait a little bit before I post pictures of what it's like there. Most of the surroundings of our building are full of dust, and entire new buildings are being built, so it's kind of a mess. For now, what I can do is show my cubicle, which is nice and spacious, and all to myself.

The only problem was, when I got there last week, there was no knob on the door. After a couple of days, one was provided to me by our wonderful administrative assistant (secretary?)... but I had to install it myself. No big deal, but it was took some work because the door needed some light carpentry before the knob would fit. So here is the way it was before:

So after some light carpentry with tools a professor lent me, I laid out all the pieces of the disassembled knob and got it to fit into the door, after about 45 minutes of work:

 

 

Ta daaaa! Maybe not the best use of a graduate student's time, if you asked my professor, but I actually kind of enjoyed it. Anyway, the cubicle isn't completely ready yet, as it will get a new coat of paint (probably tomorrow) and I'll also get a bookshelf. For now, it looks like this:

 

I'm sure it will be nice an cozy in a few days, after I get more of my stuff there and am fully settled in. In the background, you can see new whiteboards, still in their packaging, that each of the cubicles will get once the painting is finished. With one of those and the bookshelf, I'll be ready to spend most of the next three years of my life in there, doing physics. Yay!

*   *   *

Speaking of physics, it looks like I'll be working mostly out of Carroll's text book (see a couple of posts back). My professor asked me to "look over it" for the next few days (graduate professors are notoriously cryptic), and I'm basically reading it from the beginning. Also, I got two other books I ordered by mail just yesterday:

 

So I'm pretty much covered for this semester, which will be devoted mostly to learning General Relativity and getting some rudimentary models to work on my computer. If I had to put a title on my thesis right now, it would be something like The Multiplication of Tiny Four-Dimensional Spacetime Triangles: a Model. For a pretty good introduction to Causal Dynamical Triangulations, which is the formal name of what I will be working on, check out this Scientific American article by the original inventors of the idea: The Self-Organizing Quantum. Basically, I'll work on a model devised by my professor and other colleagues of his to get fundamental units of spacetime spreading out on a computer model, according to the ideas presented in this paper: http://arxiv.org/pdf/hep-th/0003238.pdf (the first author is my prof). The goal is for me to understand the math well enough to translate it into code, hit Enter, and see what happens under different starting conditions. By the end of the PhD, I should have enough knowledge and code to churn out a handful of papers on the subject in addition to my thesis.

Start your engines!

So I'm finally ready to begin my actual PhD this next Monday after months of preparation, waiting, and lots of anxiety. These past couple of days were especially tiring, as I had to complete the documentation required by the university. A complicating factor was that I hadn't formally requested my Master's degree, which is a prerequisite for applying to the PhD program. Since that takes time, it's necessary to request several special permissions and extensions, as well as filing the paperwork for the actual degree.

So when I got to the CUCEI campus this Thursday, on the next-to-last day to get all the paperwork done, I found the admissions office with several dozen people already there, waiting in line:

Unfortunately for me, I had to make a stop at another office to turn in my files for my Master's degree first, which meant I would have to wait to get into the admissions line for a while. However, when I got to the degree office, they told me I needed a certificate from my undergraduate institution, which is ITESO. Also, I needed a more recent birth certificate, since the one I provided was more than three months old. And so, I had to leave and head to the Archivo (the Archive), as it's known by all in Guadalajara, and get a new birth certificate. It's one of the busiest public buildings in the city, with all kinds of people trying to get all kinds of documents for all kinds of purposes:

After that, I headed to ITESO to get the certificate, and I stopped to take some pictures along the way. It's one of the most peaceful, beautiful campuses anywhere in Mexico, and it was even greener than I remembered it from almost ten years ago, when I got my engineering degree there (click to enlarge):

When I finally got back to CUCEI and turned in the documentation to the degree guys, the admissions line had multiplied in length, and there was no way I would be able to turn everything in before they closed for the day at 3:00 p.m. (it was 2:30). I resolved to get back early the next day (the last day allowed) to finally turn all my documents in. Here is the line, pictured from left to right as it wraps around:

 

 

I finally turned in my documentation to the admissions office yesterday, after only a couple of minutes of waiting in line, and without any further requests from the staff. So I am now free at last to focus entirely on physics.