July 31, 2016

I'm sorry I'm late with this post, in case you're keeping track so far. Life gets in the way sometimes, and there's just not enough time to do everything I want to do. Anyway, I'm reading Storm of Steel, by Ernst Jünger, and it's fascinating. It's a WWI book by a German soldier who survived the entire war, often in some of the biggest battles for months at a time, and then went on to be a prolific author and die aged 102! I've read some things on WWI before, but this is another level in terms of the crudeness of the conflict. Jünger's book is famous for not editorializing much, and simply telling things as they happen. He doesn't go into the reasons for the conflict, or whether or not it was just, or any of the comments you see in other WW1 literature. He just tells, in honest detail, what the soldiers went through. I'm about halfway through at this point, and I think I'll finish it by midweek.

Thoughts for July 23, 2016

Walking with PhD buddies on our way to lunch earlier this week, one of us mentioned the various atrocious and tragic events that have happened over the last couple of weeks. One of my buddies, who is from Chile, jokingly remarked: "All of a sudden, Mexico doesn't seem that bad anymore, huh?" We all had a good chuckle, and carried on towards our meal.

There's a saying among some comedians, which I think may itself be rooted in a quote from Oscar Wilde, that to be funny one must be telling the truth. Mexico has a myriad problems, from the daily life of its citizens all the way up to macroeconomic issues. But when one looks at international headlines, at least from the comfort of a middle-class PhD student, Mexico really isn't all that bad at all.

Europe is turning into a huge 1980's Beirut or, as some others have remarked, modern day Israel. There are now constant attacks by competing islamists against Jews (largely underreported), and ordinary citizens (especially women), not to mention the large-scale attacks like the ones in Nice last week. The Middle East, it seems, has found a way to make its troubles more horrifying and, on top of that, to export them. It doesn't help that Turkey is having an Islamic Revolution of its own, and may finally descend into full islamic theocracy soon. Syria is so bad that it's barely even reported anymore, except as a tally of dead and displaced that goes up every day. As I write this, there is news of a blast in Kabul, Afghanistan, carried out by ISIS militants against a Shia protest. To top everything off, the American election is one huge joke, with a competition between a plastic candidate that will change nothing and a dangerous, narcissistic idiot on the other.

So yes, Mexico is quite comfortable for now, from where I'm sitting (big caveat there!).

Thoughts for the week, July 16

My actual PhD work is coming along slowly but steadily. I've briefly mentioned my general area of study, which is General Relativity(GR) and, in particular, an approach to Quantum Gravity known as Causal Dynamic Triangulations (CDT). I've thought of writing something about this, but I can do no better than the explanation of the subject at The Physics Mill. There's a lot of good stuff over there and Jonah, the author, is much further along this area of study than I am (I do not know him in any world, real or virtual).

I can, however, explain a little bit of what I'm trying to do or, at least, what my professor has me working on at present. The idea is that, according to a proposed model of spacetime, we can have an elementary "cell" that divides into other spacetime cells, and those cells each divide as well, and so on. Each cell is a tiny, four-dimensional spacetime pyramid called a simplex. The way to keep track of the divisions is to keep track of the vertices, which is a lot easier, since each vertex is just a point. Simplex division in this case follows a specific set of rules: for example, the distance between any two vertices has to be greater than or equal to a minimum length, \(l\). This is the consequence of insisting that spacetime be quantized, which is the whole point of what CDT is about: we want to get tiny, indivisible chunks of spacetime that, when seen from far away, look like the smooth, continuous spacetime that GR describes.

My job, then, is to use computational methods to put a specific model of CDT to the test. The paper that outlines this model, sadly, is behind a paywall, but related papers on the physics arxiv are here and here. Anyway, here is a preliminary result:

I know, I know, it's not very impressive—but it took hours and hours of coding! An obvious remark would be that this is only a three dimensional spacetime, since that's what can be plotted in an image. This 3-D version of spacetime is a proxy for the real, 4-D thing that can't be visualized. The radius of the sphere that contains the vertices increases by a magnitude equal to the minimum length \(l\) at each step, and each step is a quantum "tick" of time. The mechanism by which the points divide is by "mating" with other points according to a specific operation and generating a new point at the new radius. All points mate with all other points, and the resulting points are located on the next sphere. This creates an enormous number of points that can't possibly fit on the surface of the sphere and maintain the condition that the distance between them is at least \(l\), so points are eliminated one by one until this condition is met (you can see the number of points in each stage at the top of the figure).

*   *   *

On completely different topics, this has been a tumultuous week. There was the attack in Nice, France, and the attempted military coup in Turkey. I wish I could write about these events, but I'm still overwhelmed by the amount of information to be digested in order to write something worth reading. 

Weekly thoughts, July 8: Gun control

In case you are interested, the view from Mexico about the gun control situation in the U.S. is, actually, not that trivially aligned with that of the wider world. I am an atypical Mexican in that I follow political and social developments in other countries closely, especially in the anglosphere. There's a common stereotype that Americans know nothing of the outside world, but I can assure you, if you're an American reader, that Mexicans are comparably ignorant about or--perhaps understandably--busy with other things besides world politics. So I can give a detailed picture about what I think, for what it's worth, but only some general remarks about Mexican society.

First, I find it scandalous that nothing has been done about the problem at all.  One would think that even the most rabid gun nut would acknowledge that something has to be done, but they actually double down and insist on "the cost of freedom" or some other platitude, and sometimes simply quote the final four words of the Second Amendment, "...shall not be infringed!", as if that were a knock-down argument for any gun control.  The trivial reply from someone like me would be, "well, then change what your stupid second amendment says!" It just seems incredible that, in the couple of decades that I've been paying attention, nothing has been done at all. Indeed, things have gotten somewhat worse since the assault weapons ban expired in the late 90's: yes, assault weapons account for only a tiny percentage of deaths, as most are due to handguns, but that's no consolation to the people in Aurora or Orlando. Yes, I understand how lobbying works and that the NRA does a lot of it; yes, I know there's a "gun culture" in the US that's different from that in some European countries with widespread gun ownership; yes, I know there are 300 million guns already out there and prohibition will create a black market and all of that; and yes, obviously some components of the problem are due to mental illness and religious terrorism; but still, the answer from Americans is we should do nothing?

From what I understand, most Americans actually do want to do something, like basic background checks before gun purchases and closing the gun-show loophole. But these things don't even get discussed at the political level because the gun nuts are very well organized in their lobbying via the NRA. I don't see Americans mobilizing en masse to do some effective lobbying of their own, as this would require a broad spectrum of warring groups in the culture war to cooperate extensively. Perhaps they could rally behind a strong presidential candidate with lots of political capital, but then that's not going to happen in this election. Over 30,000 annual deaths, plus the high-impact mass shootings we see every few months, have simply not been enough to get legislators to grow a pair and do something.

This sentiment of bewilderment at the situation is shared by most educated people in Mexico, though many laypeople who read of the latest mass shooting simply shrug it off with "Well, we all know Americans are crazy. So of course one of them would walk into an elementary school and kill 20 kids and their teachers at some point. That's just what Americans do." There is another strand of thought, if we could call it that, that seems to want to have something like the 2^nd amendment here in Mexico. Gun ownership by citizens is regulated in theory, with citizens being able to own handguns up to a .38 caliber. Everything else is deemed "for exclusive use of the army." Very few Mexicans go through the hoops necessary to get legal ownership of a gun, though those hoops are purely bureaucratic and have nothing at all to do with training in the use of firearms.

In practice, Mexico is flooded with illegal guns, which come mostly from the US and are owned by the cartels. There have been cases of .50 caliber machine guns, grenades, and rocket launchers found in the hands of the narcos; they usually out-gun the police and sometimes even the army. Still, ordinary citizens tend to shy away from gun ownership, except for the small but growing group that I mentioned above: these people, usually right-leaning or anarchist, speak of "the people" taking arms and overthrowing the corrupt government, as they perceive that every other thing has been tried already and failed. There is also a strong current of vigilantism that advocates for citizens doing police work, as police in Mexico are generally regarded as worse than the criminals.

I don't think these Mexican NRA-types will have anything in the form of political success anytime soon, but I do worry about the vigilantism they inspire. There are already cases of mobs lynching suspected criminals, and there's no way that could get any better if the mobs were armed with guns instead of pitchforks. Politicians, especially at the local levels, have already been subject to attacks usually attributed to organized crime. I can't see how that would get any better if any Joe Schmo (or Juan Pérez, rather) could do the same as well. Domestic violence deaths, suicides, and accidents would obviously increase, too. I'm by no means a pacifist--I'm just squeamish about people self-righteously appointing themselves as "good guys with guns" with no one even writing their name down somewhere.

Weekly Summary: July 1, 2016

I’m done with chapter 3 in Carroll’s book, although I still have to go through the problems at the end. Some of these will be quite tricky, if the problems in previous chapters are any indication. I already got quite a workout from following the explanations in the text, as Carroll leaves lots of details up to the reader. In particular, I spent a couple of days trying to understand the derivation he makes of the Riemann curvature tensor, \(R^{\rho}_{\,\,\sigma \mu \nu}\). This tensor completely defines the curvature of a surface, and a space is geometrically flat when it equals zero. This tensor is one of the main players in General Relativity, and is defined as \[ R^{\rho}_{\,\,\sigma \mu \nu} = \partial_{\mu}\Gamma^{\rho}_{\sigma\nu}-\partial_{\nu}\Gamma^{\rho}_{\sigma\mu}+\Gamma^{\rho}_{\lambda\mu}\Gamma^{\lambda}_{\sigma\nu}-\Gamma^{\rho}_{\lambda\nu}\Gamma^{\lambda}_{\sigma\mu} .\]

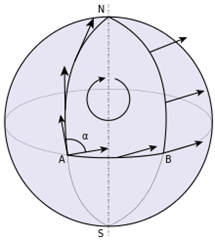
I stole the image here from the Wikipedia article to ilustrate the concept of parallel transport: you start out with a vector at a point A, as in the picture, and keep the vector pointing along the path you follow along the surface (here, northward along a meridian on a sphere). If you then turn towards another path and make your way back to your starting point, you will find that on a curved surface the vector you dragged along has been rotated. This happens in surfaces that are intrinsically curved, and the Riemann tensor is a measure of that curvature. Typically, the strategy to derive \(R^{\rho}_{\,\,\sigma \mu \nu}\) is to imagine doing the parallel transport along an infinitesimal rectangular area, as is done in the book by Schutz. Carroll, however, goes for a more direct, but also much more abstract derivation: if you have the commutator of a covariant derivative acting on a vector field, you end up with a neat expression, after some work, that includes the Riemann tensor as part of the result: \[ [\nabla_{\mu},\nabla_{\nu}]V^{\rho} = R^{\rho}_{\,\,\sigma \mu \nu}V^{\sigma} – 2\,T^{\lambda}_{\,\,\,\mu \nu}\nabla_{\lambda}V^{\rho} .\]

The term \( T^{\lambda}_{\,\,\,\mu \nu} \) is the torsion tensor, which was previously introduced in the chapter. So what we have is that when taking the (covariant) derivative of a vector field in two different directions, it matters which direction you pick first. This only happens in curved spaces, where you end up with vectors being tilted with respect to the direction they had when they first started out. Carroll does the demonstration of this in three lines, and hand-waves a bit about how to get from one line to the next. So, I took it as practice to reproduce the derivation myself, and found I was successful, without the aid of the text book, after three attempts. Typing the whole thing would be impossible here, but fortunately I did take a picture (click to enlarge):

The definitions for the covariant derivatives of vectors and one-forms are in the box in the upper right corner, and the derivation begins on the upper left. On the lower left is just a reminder to myself of the definition of an anti-symmetrized tensor, which I used in the next-to-last line. The whole thing took about half an hour, with constant erasing and starting over at several points—as it should be. A valuable lesson, then, is that following the text and constructing the arguments yourself pays off in valuable practice; you can anchor your results in the steps that the author does show, and work out the entrails of the calculation yourself. As an added bounus, often times the end-of-chapter problems ask you to “fill in the missing steps in the derivation of equation X”, so you can tick problems off your set (indeed, I have been able to check many problems in Schutz’s book off my list this way).